Методические рекомендации изложения темы «Проценты » по учебному комплекту под редакцией Г.В. Дорофеева для V – IX классов

Второй этап в изучении процентов связывается с десятичными дробями. После изучения десятичных дробей и операций над ними нужно снова возвратится к понятию процента. Здесь предлагается два специальных пункта. В пункте «Главная задача на проценты» школьники учатся находить процент величины умножением на десятичную дробь. Прежде чем приступить к решению задач, нужно рассмотреть с учащимися правило и упражнения на перевод процентов в десятичную дробь.

«Чтобы выразить проценты десятичной дробью, нужно число, стоящее перед знаком %, разделить на 100 или, что то же самое, умножить на 0,01»

№ 596.[15] Выразить десятичной дробью:

а) 2,5%, 18,3%, 1,6%, 54,5%;

б) 0,1%, 0,5%, 0,3%, 0,7%;

в) 120%, 137%, 240%, 350%.

Предлагается рассмотреть разные способы решения той или иной задачи.

Пример 2. Мужская рубашка стоила 8200 р. Сколько она стала стоить, когда ее цена увеличилась на 35%?

Так как 35% – это 0,35, то надо найти 0,35 от 8200 р.:

(р.) (на столько повысилась цена).

Теперь найдем новую цену:

8200+2870=11070 (р.).

Можно рассуждать иначе. Старая цена составляет 100%, а новая – на 35% больше, т.е. она составляет 135%. Так как 135% – это 135:100=1,35, то цена увеличилась в 1,35 раза.

Имеем: (р.).

Также учащиеся знакомятся с задачами типа К2. Но авторы рассматривают эти задачи в рамках упражнений группы Б (более сложных).

№ 606. В первый час работы продавец продал 40 кг яблок. Это составило 16% от первоначального количества яблок. Сколько килограммов яблок было у продавца первоначально?

В пункте «Выражение долей в процентах» центральной является задача об определении того, сколько процентов одна величина составляет от другой.

619. В избирательном округе 2500 избирателей. В голосовании приняли участие 1300 избирателей. Какой процент избирателей участвовал в голосовании?

Здесь принят подход, в соответствии с которым сначала находят, какую часть одна величина составляет от другой, выражают ее при необходимости десятичной дробью, а затем – в процентах.

Не следует торопиться приступать к решению новых задач. В учебнике предлагается система упражнений, в которых предлагается выразить дробь (обыкновенную или десятичную) в процентах.

№ 615. Прочитайте предложение, выразив дробь в процентах:

а) бензином заполнили бака;

б) учащихся школы едут в школу на автобусе;

в) масса сушеной вишни составляет массы свежей вишни;

г) магазин продал привезенного сахара.

Одна из особенностей вычислительной линии курса состоит в формировании умений выполнять прикидку или оценку результата вычислений. При изучении процентов эта работа, естественно, продолжается. Учащимся предлагаются задачи из повседневной практики, в которых требуется найти приближенно с помощью прикидки процент от заданной величины. Для этого достаточно заменить данные другими числами, близкими к ним и удобными для расчетов. Так, если требуется прикинуть, чему равно 19% от какой-либо величины, то находят 20% этой величины, т.е. ее пятую часть.

№ 595. Перед Новым годом магазин снизил цены на товары на 25%. На сколько примерно рублей понизилась цена товара, если до снижения она составляла 799 руб.? 1980 руб.? 11890 руб.?

№ 629. Часть фигуры заштрихована (см. рис 4.). Определите, какой примерно процент фигуры заштрихован, выбрав наиболее подходящий ответ из данных.

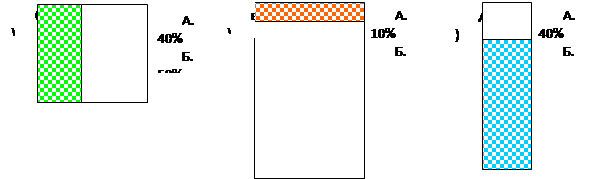
Рис. 4

Третий этап в изучении процентов отнесен к 7классу. В силу возрастных возможностей семиклассников и уже накопленного ими опыта работы с процентами учащимся становятся доступными многие вопросы из тех, что традиционно не рассматривались со всем классом, а изучались лишь в качестве дополнительных в работе с сильными учениками. Учащиеся уже знакомы со всеми основными видами задач, теперь они осваивают другие способы их решения, которые были им неизвестны.

В первой главе учебника выделен пункт «Решение задач на проценты», в котором помещен материал, позволяющий вспомнить сведения из шестого класса и продвинуться в решении задач. Теперь есть возможность рассмотреть более сложные в техническом отношении задачи. Они требуют достаточно прочного навыка представления процентов дробью и наоборот, умение находить процент от величины, понимание того, какая из величин, участвующих в задаче, принимается за 100%. Поэтому в начале теоретической части пункта рассматриваются приемы, с помощью которых десятичная дробь выражается в процентах и наоборот; здесь специально выделяется вопрос о «маленьких» (меньше 1%) и «больших» (больше 100%) процентах, как наиболее трудный для усвоения.

Еще по теме:

Значение игры в системе обучения
Как показывает опыт работы, необходимым условием эффективности развития художественного творчества детей является введение в структуру уроков изобразительного искусства отдельных игровых элементов и художественно-дидактических игр и использование элементов соревнования. Значение этого условия предо ...

Ценностное отношение к обществу
Ценностное отношение к обществу – столь же последовательный и поэтапный процесс. Общество выступает для ребенка сначала в виде общепринятых нормативов, регуляторов его поведения в социуме. Затем раскрывается для него связь текущей жизни за счет распределения социальных ролей Человека в обществе. По ...

Современные представления о развитии личности детей с 3ПP
Внимание исследователей и практиков (педагогов, психологов, врачей) в первую очередь привлекают дети с наиболее выраженными нарушениями развития, прежде всего с глубокими формами интеллектуальной недостаточности, затем - умственно отсталые. По мере развития общества, а вместе с ним и науки, в том ч ...

Категории

• Главная
• Обучение детей ориентировке во времени
• Половое воспитание детей и подростков
• Ценности и воспитание
• Работа социального педагога
• Предмет и задачи педагогики
• Теоретические основы воспитания
• Информация о педагогике и образовании
• Карта сайта
• Контакты